- Головна
- Готові шкільні презентації
- Презентація на тему «Теорія ймовірності» (варіант 3)
Презентація на тему «Теорія ймовірності» (варіант 3)
263
Поділитись підручником в соціальних мережах
Слайд #1
Теорія ймовірності

Слайд #2
Теорія ймовірностей — розділ математики, що вивчає закономірності випадкових явищ: випадкові події, випадкові величини, їхні функції, властивості й операції над ними.

Слайд #3
Виникнення теорії ймовірностей як науки відносять до середніх століть і першим спробам математичного аналізу азартних ігор.

Слайд #4
Теорія ймовірностей є підґрунтям математичної статистики. Широко вживається для опису й вивчення різноманітних технологічних процесів зважаючи на їх стохастичність.

Слайд #5
Як і будь-яка інша математична теорія, теорія ймовірностей будується на основі деяких основних понять, відношень та означень. За їх допомогою формулюються основні правила, закони, теореми.

Слайд #6
Дослід, експеримент, спостереження події називають випробуванням. Результат, наслідок випробування називають подією.

Слайд #7
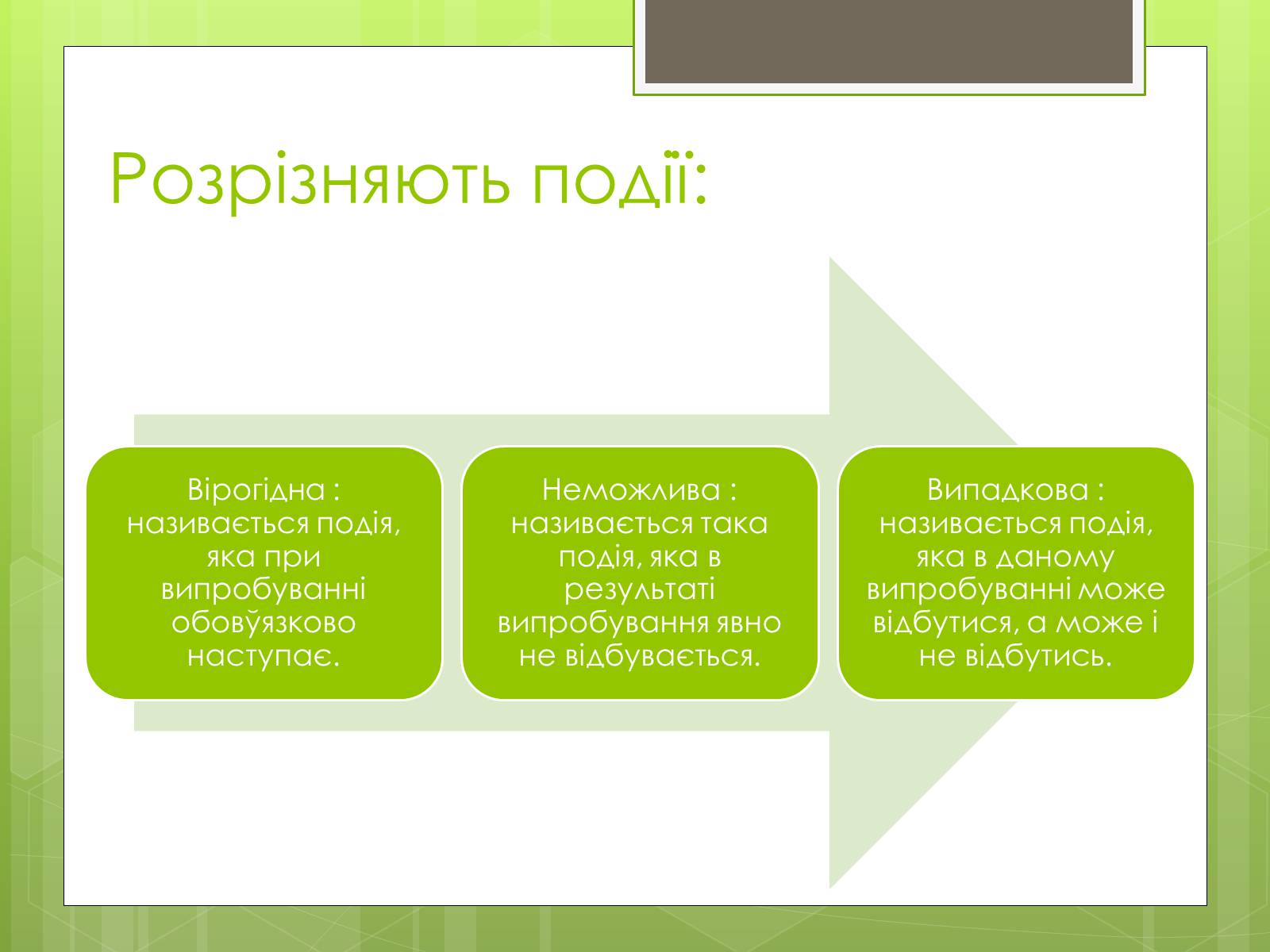
Розрізняють події:
Слайд #8
Дві події називаються сумісними, якщо поява однієї з них не виключає появи іншої в одному й тому самому випробуванні.
Дві події називаються несумісними, якщо поява однієї з них виключає появу другої в одному й тому самому випробуванні.
Дві події називаються несумісними, якщо поява однієї з них виключає появу другої в одному й тому самому випробуванні.

Слайд #9
Дві події А і В називаються протилежними, якщо в даному випробуванні вони несумісні й одна з них обовўязково відбувається.

Слайд #10
Імовірність - числова характеристика можливості появи випадкової події за певної умови, яка може бути відтворена необмежену кількість разів.
Імовірністю випадкової події називається відношення кількості подій, які сприяють цій події, до кількості всіх рівноможливих несумісних подій, які утворюють повну групу подій під час певного випробування.
Імовірністю випадкової події називається відношення кількості подій, які сприяють цій події, до кількості всіх рівноможливих несумісних подій, які утворюють повну групу подій під час певного випробування.

Слайд #11
m - число елементарних подій, які сприяють події А;
n - загальна кількість рівноможливих і несумісних подій, які утворюють повну групу.
n - загальна кількість рівноможливих і несумісних подій, які утворюють повну групу.

Слайд #12
У теорії ймовірностей розрізняють прості і складені події.
Подія називається складеною, якщо поява її залежить від появи інших, простих подій.
Обчислювати ймовірності складених подій за формулою буває важко, а іноді навіть неможливо. Їх імовірності обчислюють через імовірності простих подій з яких складаються складені. Таке обчислення спирається на застосування теорем додавання й множення несумісних однаково можливих подій, які утворюють повну групу, тобто елементарних подій.
Подія називається складеною, якщо поява її залежить від появи інших, простих подій.
Обчислювати ймовірності складених подій за формулою буває важко, а іноді навіть неможливо. Їх імовірності обчислюють через імовірності простих подій з яких складаються складені. Таке обчислення спирається на застосування теорем додавання й множення несумісних однаково можливих подій, які утворюють повну групу, тобто елементарних подій.
